1. 검정력 분석(power analysis)
유의수준 α, 표본크기n, 표본분산s, 효과크기, 검정력(1- β)이 고려된다.(1종오류 α, 2종오류 β에 대해서는 이전 글 참고)
G*power를 이용한 검정력 분석에서는 "post hoc: compute achieved power - given α, sample size, and effect size"를 선택하여 검정력을 알아볼 수 있다.

1. independent t-test, post hoc 설정
2. determine 클릭하면 3번 창이 나타남
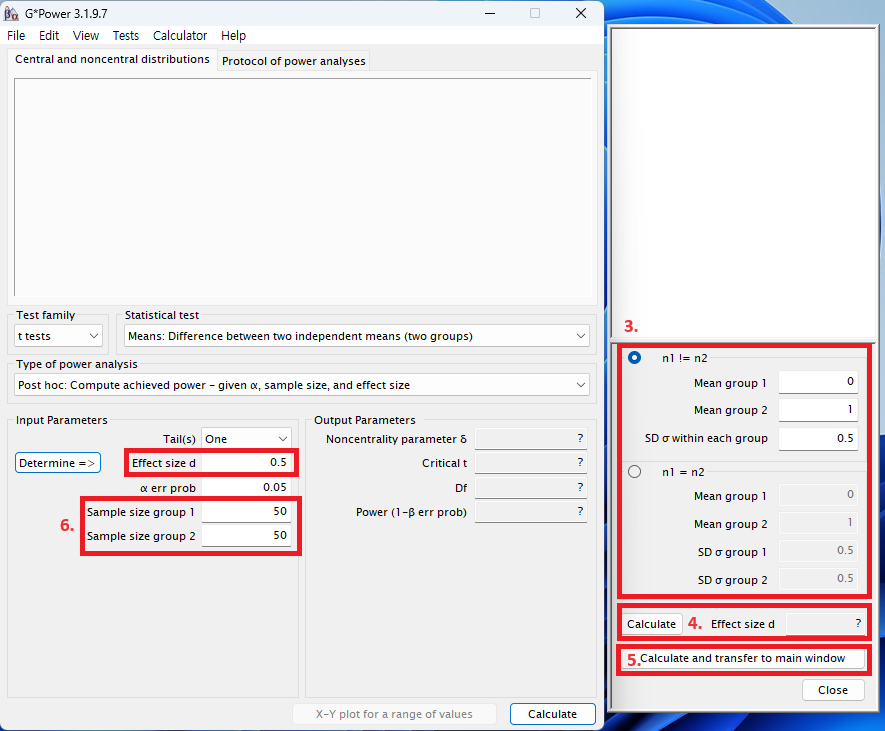
3. 두 변수 샘플사이즈가 다르므로 첫번째 n1!=n2를 선택 ( 두 샘플 사이즈 같으면 아래 n1=n2 선택)하고 각 그룹의 평균을 입력, SDσ within each group 계산하여 입력 이때 필요한 Pooled Standard Deviation 구하는 공식은 다음과 같다.

4. calculate을 누른다음 Effect size d가 나타나면
5. calculate and transfer to main window를 클릭하면 메인창에서 Effect size d가 입력됨
6. 각 그룹의 샘플 사이즈를 입력하고
마지막으로 calculate 버튼을 눌러주면 오른쪽 Output Parameters에서 검정력(power, 1- β )를 알 수 있다.
2. 효과크기(effect size)
: 차이의 정도 또는 관련성의 정도를 측정하는 것이다.
- 피실험자의 수가 적거나 많은 경우 일어날 수 있는 통계결과의 왜곡을 보완해주는 역할을 한다.
- 메타분석(meta-analysis)에서 서로 다른 표본크기(sample size)를 가진 서로 다른 연구들을 비교할 수 있다.
- 효과크기 지수(effect size index) : t, F, r처럼 단위 없이 모든 종류의 데이터에 적용할 수 있도록 표준화된 값을 사용하여 효과크기를 나타내는 통계량
- 관찰된 효과 차이가 크면 클수록 같은 유의수준 하에서 통계학적으로 유의할 가능성이 커진다.
* 연구가 끝난 후에는 표본크기, 분산, 평균, 상관계수 등을 알 수 있고 이러한 정보들을 이용해서 검정력의 정도를 구할 수 있다.
* 상관관계 연구에서 적어도 r=0.6 정도면 의미가 있다고 정할 수 있다.
3. 표본크기(sample size)
연구자가 데이터 수집 전에 표본크기를 정하고자 하지만 기존의 자료가 없을 때 Cohen이 사용한 수치를 사용할 수 있다.
Cohen's d
| d = (집단1의 평균 - 집단2의 평균)/표준편차 |
.2이면 작은 효과(small effect)
.5이면 중관 효과(median effect)
.8이면 큰 효과(large effect)를 가진다고 한다.
독립t-검정& 등분산일 경우↓
| d = t값√(n1+n2)/(n1*n2) |
이 계산식에 근거하여 검정력을 구하려면 Cohen의 표를 이용한다.
하지만, 직접 계산 할 필요 없이 G*Power라는 프로그램을 이용하여 원하는 검정력의 표본크기를 구할 수 있다.
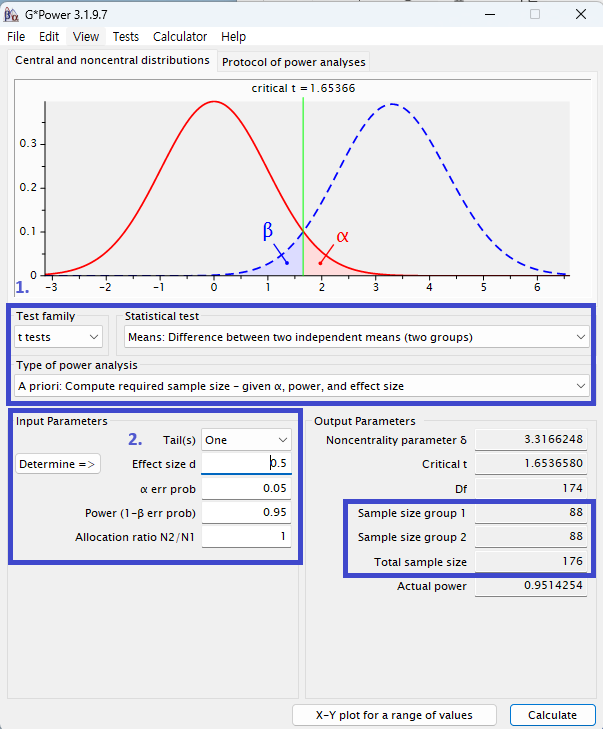
1. independent t-test에서 표본크기를 구하기위해 A priori:~를 선택한다.
2. 방향성이 있으면 one tail test(단측검정), 방향성이 없으면 two tails test(양측검정)로 선택하고 유의수준과 원하는 검정력을 입력하고 두 집단의 샘플 사이즈를 같게 하려면 ratio를 1로 설정한다.
3. Calculate를 누르면 계산되어 나온 output parameters에서 Total sample size와 그 아래에 actual power를 구할 수 있다.
예를들어 영가설(귀무가설)을 A치료와 B치료의 효과는 차이가 없을 것이다.
대립가설(연구가설, research hypothesis)로 A치료보다 B치료의 효과가 더 클 것이다. 라고 가정한다면
B치료의 효과가 더 클 것이라는 방향성을 제시했으므로 One tail
만약 대립가설로 A치료와 B치료의 효과에는 차이가 있을 것이다. 라고 가정한다면 방향성이 제시되지 않았으므로 Two tails로 설정하고 진행하여야 한다.
유의수준은 적어도 0.05로 설정해야한다. (유의수준과 검정력에 대한 설명은 이전 글 참조)
검정력은 0.8이상으로 설정해야 한다.
'연구방법론' 카테고리의 다른 글
| 다중비교(multiple comparison)와 반복측정 분산분석(Repeated ANOVA) (0) | 2024.06.20 |
|---|---|
| 추측통계학: t-검정(t-test)과 분산분석(ANOVA) (0) | 2024.06.20 |
| 가설검정(Hypothesis testing or significance testing)과 가설검정의 오류 (0) | 2024.06.20 |
| 표본추출과 표본분포(Sampling and sampling distributions)(추정, 표본 평균 분포, 표준 오차) (0) | 2024.06.20 |
| 기초통계학 정리(기술통계, 추론통계, 정규성검정 etc.) 및 순서 (0) | 2024.06.20 |

